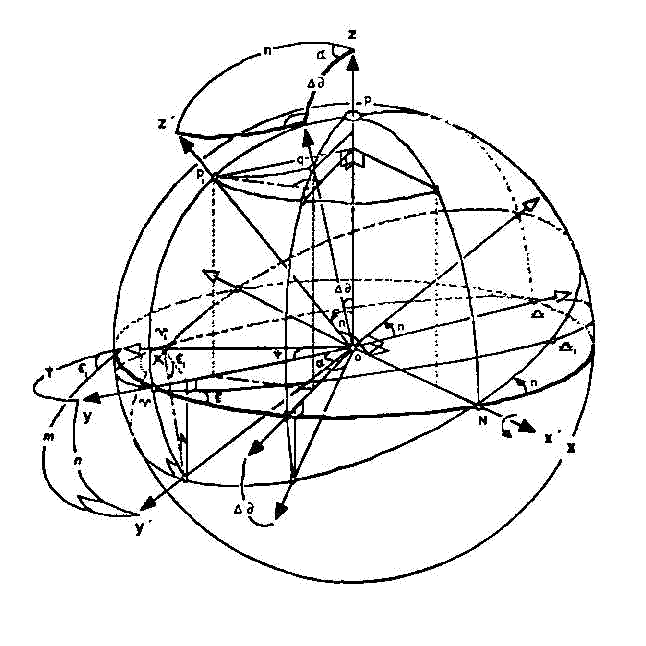
__

At first sight, my diagram may appear to be the work of a fevered mind, but it is an accurate depiction of the complex geometry underlying the precession of the equinoxes. Simply put, precession is the wobbling of the Earth's axis, which takes place over many thousands of years.
     Our planet's axis of rotation does not always point to the North Star; it slowly alters direction in space, much like the handle on a spinning, wobbling top. This alteration in direction brings about changes in the coordinates of fixed celestial bodies such as stars. Declination is the name of one such coordinate in the sky.
     Although many textbooks in positional astronomy provide formulas for calculating the change in coordinates due to precession, not a single one I've found shows in much detail the geometry behind these changes. This then may be the first comprehensive illustration showing how the declination of a fixed star changes as a result of precession, specifically that part of precession caused by the combined pull of the Sun and Moon on the Earth.
    After obtaining a stack pass to Deck 9-North of The Library of Congress, I sifted through one of the largest collections of astronomical texts in existence, searching for the kind of diagram I finally had to make myself. I did it quite a few years ago, on an old 512K Macintosh using very unsophisticated software. It took me about three weeks to finesse all the lines and labels into place.
    Is my diagram perhaps too detailed? Very likely. Just as in a computer program, in a technical drawing, information takes up room. I could have left out numerous elements in the diagram, but having been enormously peeved by the sketchy graphics in so many math and science books, I set out to see how much data I could overlay in one diagram. I will always err on the side of excess rather than leave out visual clues that could help explain why an equation works.
    I regard geometry as a very visual subject, which algebra reduces to a kind of language, to a shorthand and summary of the essentially pictorial. In order to really appreciate algebra, we must get behind the symbols to the geometric facts which algebra proves and describes—Omar Khayyam said as much nine hundred years ago. I hope to reclaim what is visual in math, namely the geometry behind algebra. I say that a geometric drawing is worth a thousand algebras!
    Often it has been said that "mathematics is the language of science." That has too long been the analogy, and a false one. Mathematics is far more a picture than a language. I would rather say that "algebra is a language describing geometry, a picture." We might think of it this way: the words "a skylark soars over a wheatfield" is an algebra—the shorthand and summary of a geometry, van Gogh's Field With Lark.
    The great Enlightenment astronomer and mathematician J. L. Lagrange actually prided himself in using no illustrations in his texts. This anti-pictoral bias has been adopted by mathematicians ever since. Today, you can't find a book on, say, Hilbert Space or vector calculus which contains good visualizations—I mean illustrations that actually link the algebraic equations to the geometry. This makes learning what is going on "behind the equations" unduly difficult.
     I believe that mathematics, far from being a highly conceptual field, is really as visual a subject as art history.